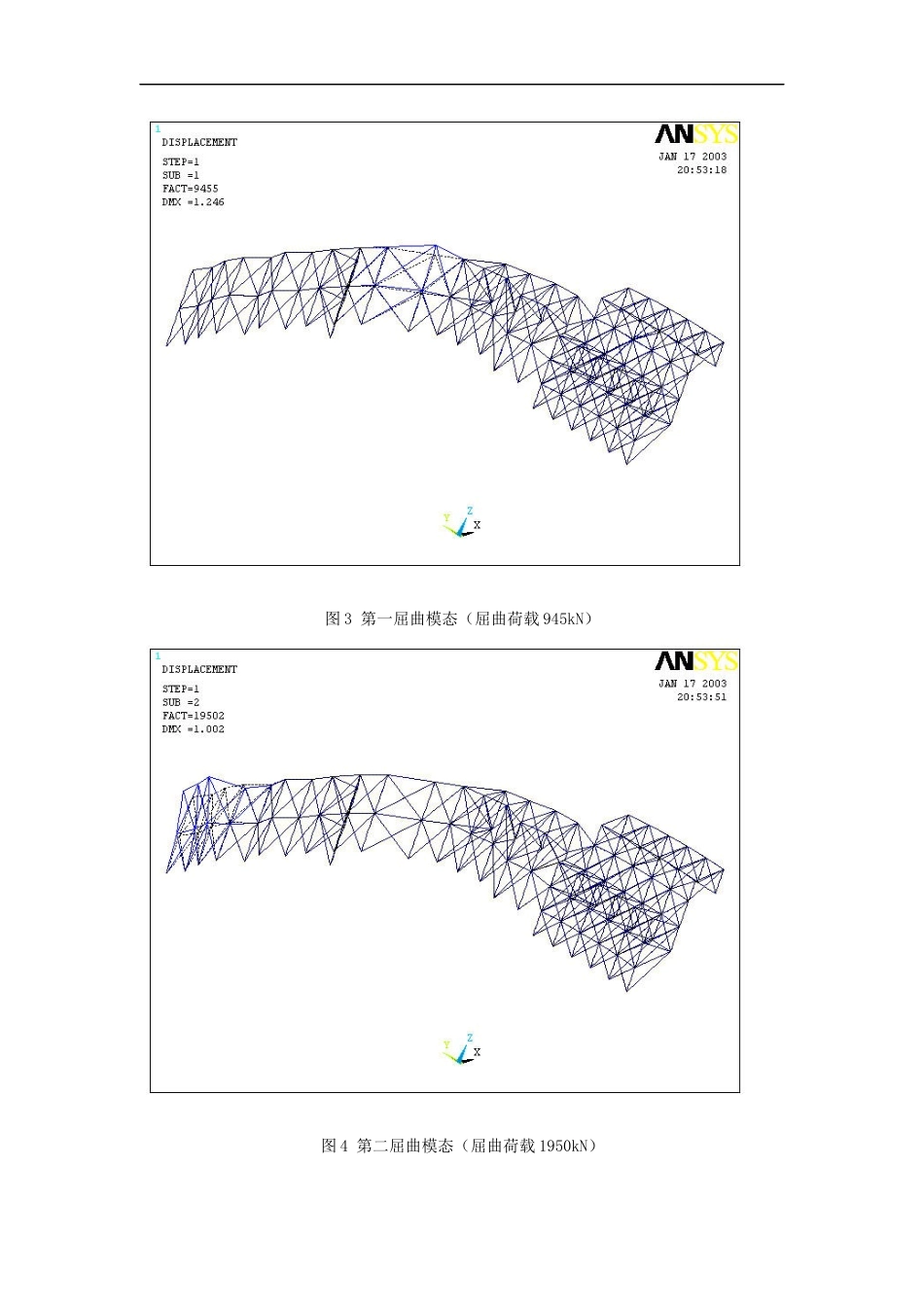
江苏某体育场钢结构吊装工况分析在钢结构安装过程中有如下工况需要分析:①安装用支承台架的稳定性分析;②结构体系的变形分析;③卸载过程的力学分析。1.安装用支承台架的稳定性分析1.1 屋面支承台架1.1.1 屋面支承台架的布置屋面支承台架采用壁厚 12mm、外径 609mm 的钢管,在四分之一体育场范围内共有四十个支撑点,上部支承屋面箱梁,下部固定于混凝土看台结构。钢管支承台架之间采用槽钢在水平向和斜向拉接,布置图见图 1;图 2 是支承台架与屋面箱梁的位置关系示意图。根据计算,在施工和支撑卸载过程中,屋面支承台架可能受到的最大轴力为 500kN。图 1 支撑布置图图 2 箱梁与支撑位置关系1.1.2 计算模式采用 Ansys 程序计算上述支承系统的稳定性,计算内容包括系统的理想状态分支失稳模态和考虑缺陷和材料非线性、大变形的非线性稳定分析。图 3~图 5 为结构承受台架顶部集中力作用下第 1~第 3 阶失稳模态,其后几阶模态与前三阶模态有类似的表现。失稳模态揭示了在东西向箱梁下的台架由于一个方向没有约束而比较容易产生失稳,这与实际情况相符合。计算表明第一阶模态下的屈曲临界荷载为945kN。图 3 第一屈曲模态(屈曲荷载 945kN)图 4 第二屈曲模态(屈曲荷载 1950kN)图 5 第三屈曲荷载(屈曲荷载 2659kN)非线性稳定分析的计算模型采用一致模态法建立。按照第一失稳模态的位移模式,该模型考虑了最大处 3cm 的初始误差。材料屈服应力取为 210MPa。图 6 为在结构施加递增荷载时,最大位移点的侧向位移曲线。从该曲线可以知道,结构在 725kN 时开始发生屈曲,而最大可承受荷载为 1070kN。在承受额定的 500kN 时,侧向变形为 27mm。图 7 为最后位移不收敛状态前,将要屈曲支撑的应力分布图。图 8 为屈曲发生前的结构位移图。屈曲杆件与理想状态模态分析一致。图 6 非线性稳定结果:分析轴力-位移关系图 7a 非线性稳定分析:屈曲杆件应力(单位:10e-6Mpa)图 7b 非线性稳定分析:临界状态支撑系统应力分布(单位:10e-6Mpa)图 8 屈曲临界状态变形图1.1.3 计算结果上述计算表明,屋面箱梁下部支承台架具有足够的结构稳定性以承受施工、分步卸载过程中的支撑轴力,稳定安全系数在 1.45 以上。1.2 主拱支承台架系统1.2.1 支承台架布置主拱支承台架系统由桁架结构构成,平、竖撑为 L140×140×14 的角钢组成,斜撑为L60×60×8 的角钢组成,每组支承台架由两个空间桁架支撑拱段重量,1、2、3 号台架旁边并配有类似桁架组成的操作平台,并作为主支承台架的稳定体系。台架下部用大型钢梁将竖向荷载直接传递给相邻的混凝土柱,上部采用三点与主拱相接。选取典型的 2 号台架进行了稳定计算,台架图为图 9,台架与主拱、相邻箱梁的位置关系见图 10。图 9 2 号主拱支承台架计算模型图 10 主拱支承台架与主拱、箱梁位置关系1.2.2 稳定计算与屋面支承台架一样,对主拱支承台架进行分支屈曲模态分析和非线性稳定分析。在分支屈曲模态失稳分析中,按照三个支承点实际情况中受力大小的比例关系,在支承点处施加初始荷载,并籍此进行屈曲分析,图 11 是该项分析得到的第一失稳模态,其临界荷载为 3830kN。图 11 第一失稳模态在非线性稳定分析中,材料屈服应力取为 210MPa,考虑与第一模态相似的初始位移干扰,最大干扰位移为 40mm。在支承点施加的三个集中力数值之间的比例关系按照支撑受力时的实际情况进行施加。图 12 是台架顶点侧向位移与支撑总反力之间的关系,在总荷载达到 1277KN 时,计算结果不收敛,说明支承台架结构不能继续承载。图 13 时临界状态的变形图。由图 13 可见,非线性计算得到的变形与模态分析得到的一致。图 14 反应了临界状态应力分布。从图 14 可见,临界状态支撑的角部构件基本上整体受压,全截面达到材料屈服,从而导致结构丧失稳定性。正是由于材料屈服,使得非线性计算得到的临界荷载比模态失稳分析得到的小得多。图 12 支承台架系统顶点侧向位移与台架总反力关系图 13 非线性分析的临界变形图 14a 临界状态台架杆件应力分布(单位:10e-6Mpa)图 14...